(click here for introduction and part 1) (click here for part 2)
MODELS IN PRACTICE
1. THE MODEST STATUS OF MODEL ASSUMPTIONS
Consider the following problem given to a high school physics class:
You drop an object from an altitude of 100 meters. How long will it take for the object to reach the ground? Assume there’s no air resistance.
What does the teacher mean when she asks her students to ‘assume there’s no air resistance’? Is she telling them, literally, there is no air resistance?
Of course not. The point of solving a simplified problem such as this is to understand how gravity works. Ignoring all other forces acting on a falling object allows the students to isolate the effect of gravity. In a real-life situation you would have to take all forces into consideration (using Newton’s laws of motion), but this simple problem is a good starting point for more realistic ones. Assumptions can be relaxed and further complexity can be added later on, as the students get a better understanding of the subject. In fact, instead of saying ‘assume…’, the teacher could have said ‘ignore air resistance’. It’s the same instruction, but the word ‘ignore’ makes it clear that the assumption of no air resistance is false, strictly speaking.
An explicit assumption is generally something the modeler doesn’t actually believe in. Quite the opposite, in fact; the assumption is mentioned precisely to warn the reader that a practical implementation requires adjusting the model or supplementing it with others. (Critics who imply that the originator of a model dogmatically believes in the literal truth of her assumptions are either totally ignorant of practical modeling or just disingenuous.)
We can formalize the students’ model as follows:
g = 9.8 m/s2 [1]
‘g’ denotes the gravity of Earth. The value of 9.8 m/s2 means that the speed of an object falling freely near the Earth’s surface increases by about 9.8 meters per second every second. That statement reveals two important assumptions:
-
“falling freely“: this is the assumption that there are no other forces (e.g. air resistance)
-
“near the Earth’s surface”: actually, g decreases with altitude, but for relatively low altitudes, the constant value is a good approximation.
If skeptical Tony complains you can’t use the law of gravitation “because it assumes there’s no air resistance”, tell him the law still works, he just has to add the force of air resistance. Every physics undergraduate can do it, so why can’t he?
Now to finance. Fischer Black and Myron Scholes used a number of assumptions in the derivation of their famous Black-Scholes option pricing formula. For example, that the underlying stock pays no dividends, or that there are no trading costs for either the stock or the option. To poorly informed commentators, this is clear evidence that the two were ivory-tower academics, with no common sense or practical knowledge of financial markets. Nothing could be further from the truth.
As with the physics example above, the very fact that Black and Scholes made their assumptions explicit showed that they were aware of their being unrealistic. Stating their assumptions was like saying: ‘we’re ignoring trading costs etc.’. Besides, it was none other than the late Fischer Black himself who wrote an article titled The Holes in Black-Scholes (Risk 1, no. 4, 1988), pointing out the imperfections of the model. In a later revised version (How to use the holes in Black-Scholes, Journal of Applied Corporate Finance, 1989, vol. 1, issue 4), he even referred to the formula as the Black & Holes formula (demonstrating his sense of humor too was more developed than that of many of his critics).
The Black-Scholes formula can easily be extended to options on dividend-bearing stocks. So the assumption of no-dividends is just as unimportant as the assumption of no-air resistance in the physics example. Trading costs are more complicated. But in any case, Black and Scholes provided an extremely useful framework allowing traders to relax unrealistic assumptions and add more complexity depending on their needs. Many later option formulas by other authors are extensions of Black-Scholes (e.g. the Garman–Kohlhagen model for FX options). You see, all models make explicit assumptions that constrain their validity. But the constraints are not always, um… constraining. Unrealistic assumptions are no real barrier to using a model in practice, because they can easily be relaxed in more realistic extensions.
Another reason why researchers make assumptions in a publication is to derive a particular solution to a certain problem, leaving it to the creativity and skills of their colleagues to find either other particular solutions, or a more general solution, using a similar approach as theirs. Compare it with an if-then statement: even if premise A is manifestly false, the statement if A then B can still be true. A model is usually presented as an idealization, a simplified, stylized representation that provides the essence of the phenomenon of interest, but ignores the nitty-gritty details. Idealizations make models easier to understand (a didactic reason), and easier to solve (a practical reason). They also serve to isolate the various (simple) mechanisms that, jointly, give rise to complex phenomena. As we will see, idealizations are not only acceptable in practice, very often they are unavoidable.
Needless to say, idealizations are ubiquitous in every field of science, including physics (arguably the most respected of the empirical sciences). Costless trading is an example of an idealization in finance. Examples of idealizations in physics are abundant: point masses, ideal gases, perfect fluids, frictionless surfaces, isolated systems, uniform space,… Because they are idealizations, thus imperfect representations of reality, they are apt to be disparaged as unrealistic. The important thing to keep in mind here is that the purpose of a model is not to be like a picture hanging idly on the wall, as a ‘true’ description of some aspect of the world for us to marvel at.
The purpose of a model is to function as a tool. A model has to do some work. When evaluating the merits of a model, the extent to which it accurately represents the world is of secondary importance. Most important is how good it is at doing its job. The main function of financial models is to determine asset prices (see part 2). Models can also be used for didactic purposes, as the physics problem in the introduction. The Stanford Encyclopedia of Philosophy has a very interesting entry describing the myriad ways in which models are used in science.
The model’s job may consist in generating predictions. Not 100% correct predictions, mind you, but predictions that are more reliable than wild guesses. Hence, models can be ranked according to their predictive accuracy. Sometimes models can be extremely accurate: their approximations are so close to the real thing that deviations cannot be distinguished from measurement error. Some models may be bad (worse than others), but still better than nothing. Models that try to be too accurate often become totally impractical, for reasons I will discuss in the next section.
It’s true that the best, most accurate models[2], are usually found in the so-called “hard” or “exact” sciences (like physics). But it’s a common mistake to think that all of physics shares the incredible precision of particle physics or Newtonian mechanics (at least, for medium-scaled objects, distances, and velocities). To be sure, the calculations done in fluid dynamics or complex systems theory are very precise, but the predictions that result may be rather weak, due to uncertainties in the values of parameters or variables.
If there’s a fundamental difference between finance and physics it must be this: the importance of idealizations and their role as building blocks for more realistic theories is rarely questioned in physics, while in finance you find naive commentators all the time complaining about ‘unrealistic’ assumptions. I will say more about alleged or real differences between physics and finance towards the end of this article. At this point, I just want to emphasize that I’m not implying the laws of finance are as powerful as the ones in physics. All I’m saying is that a casual inspection of assumptions is not sufficient to reject a model.
At heart of this naïve and superficial view of models is the mistaken belief that the foundations of a model are its assumptions. You know, as in buildings: if you don’t get the foundations right, the whole edifice collapses. The foundations of models, however, are not their (very often contrary-to-fact) assumptions, but something far more subtle and interesting. A good model captures the essence of the target phenomenon, it extracts the most relevant features and ignores less important ones.
As for the Black-Scholes framework[3], despite the shaky ‘foundations’ (assumptions, rather) the edifice still stands tall: it is still ubiquitous in finance despite its many imperfections. Its foundations are not the fantasies of zero transaction costs or the unlimited ability to borrow, but something else, first and foremost the principles of no-arbitrage and delta hedging, principles that are still widely used by the finance community today.
There are some assumptions in the B&S model, though, that remain controversial until today (particularly the lognormal model of asset prices), but the impact of their falsehood is often exaggerated. More on that later, for now just keep in mind that the question of whether or not an assumption holds in reality is far less essential to the model than is often suggested.
2. The return on investment from models
The American philosopher Daniel Dennett[4] has used an interesting metaphor in discussions of philosophical theories of mind, but I’ll use it in a wider context. As you’re about to find out, it’s even particularly apt in a financial context (OK, that’s a bit corny, but anyway…).
Dennett argues that a theory builder is allowed to make unverified assumptions, but not without limit. The theory builder, he says, takes out a loan, and that loan must be repaid eventually. Much as the founders of a new company have to pay back their loans, plus interest. The entrepreneurs can do so only if their company generates revenues in excess of costs. In English: if they succeed in ‘getting more out of the company than they put in’.
It’s the same with models. You put in some things you own (the verified assumptions), and some you don’t (the unverified ones). Your goal is to get more out of the model than you put in. That will happen if the model allows you to generate reliable predictions you can’t make without it. A modeler’s ability to make money (literally so in part 1 of modeling 101) depends or her accuracy rate. Initial deficit spending in the building of models is allowed, as long as debts are repaid once the model is up and running.
Now, some conservatives are radically opposed to deficit spending, but the problem is not with (temporary) deficit spending per se, the problem is with unproductive big spenders. For example, pseudoscientists typically make all sorts of claims, but avoid formal tests of them, or invariably come up with silly excuses when they’re proven wrong. There’s nothing wrong with an astronomer’s assuming Jupiter’s orbit around the sun is unaffected by relativistic effects. Her predictions of Jupiter’s position are sufficiently accurate, even though the law of universal gravitation she uses is not consistent with the theory of relativity, strictly speaking. But it’s not OK for an astrologer to invent elaborate theories of how celestial bodies affect not only our personality, but also the events that happen to us, without ever subjecting the theories to systematic tests that may prove them wrong. The astronomers are the productive entrepreneurs; the astrologers are irresponsible wasteful spenders. As Dennett comments,
“no one has ever been able to get rich by betting on the patterns of astrology, only by selling them to others.” (Real Patterns, Journal of Philosophy, Jan 1991. Reprinted in Brainchildren, MIT Press, 1998)
We can push the metaphor a little bit further. In addition to the criterion of positive return, we can evaluate a model on its return on investment (ROI), i.e. how much bang for our buck do we get if we use the model. A loan comes with a cost. The cost is the risk of being wrong. It should be compensated for by a benefit, namely a superior ease and power of prediction. If you assume asset prices follow a normal distribution, you are bound to run into problems at some point, because empirical evidence shows that asset returns are fat-tailed. But your predictions based on a simple normal distribution are much more powerful (accurate) than for example a distribution characterized by infinite variance, most of the time at least. The context is important: if your goal is to describe the behavior of asset returns in normal (= not extreme) markets, then the normal (= Gaussian)[5] distribution is usually the most useful. If your goal is to find out what could happen in a worst-case scenario, then you might switch to a heavy-tailed distribution. Pragmatism is the ultimate norm.
The ROI analogy applied to models is not just philosophical. It has a precise mathematical counterpart; that is, you can even measure – as it were – the ROI of a model (at least on a comparative basis: what is the marginal benefit of adding extra parameters to a model). That’s what the rich field of model selection is all about: how to balance goodness-of-fit (to the data) with simplicity. Using a complicated model with many parameters may lead to overfitting: the model fits the available data extremely well but it’s very poor at predicting new observations. Measuring the marginal benefit of introducing more complexity into a model is precisely what measures like the Akaike Information Criterion (AIC) aim at: they subtract the cost of extra parameters from the benefit of a better fit. Adding more parameters (more complexity) is OK as long as the marginal benefit is positive. In other words, as long as you get more bang for your buck, it’s OK to put up more buck. But at some point the marginal benefit becomes negative; which means you’ve gone too far in trying to refine your model. It’s a well-known fact among practitioners that excessive attempts at making their model perfect actually make it worse: too much refinement introduces noise[6].
What makes the normal distribution ubiquitous in science (yes, physics as much as finance or any other major scientific field), and the Black-Scholes formula in finance, is that both use a minimal number of parameters. The normal distribution has only two parameters: the mean and the standard deviation. In contrast, the stable Paretian distribution advocated by Mandelbrot and Taleb already has four. Needless to say, it’s much easier to estimate two parameters than four. The popularity of the Black-Scholes formula among option traders and other practitioners in finance has undoubtedly to do with the fact that it has only one free parameter[7], namely the volatility, whose interpretation, besides, is very intuitive. That also makes it an ideal starting point for introducing students into the theory of option pricing; it helps them understand what variables affect option prices and in what way. Familiarity with Black-Scholes as well as awareness of its limitations are also extremely useful when analyzing the more problematic cases.
There’s another keyword worth mentioning here: tractability. In order to be useful in practice a model must be tractable. There’s no point in using an extremely sophisticated model if it takes you hours and hours to calculate its parameters and to solve the problems it’s supposed to solve. Quick-and-dirty is much more useful than clean-but-hopelessly-slow. It’s quite ironic that many detractors of Black-Scholes and the normal distribution complain that they are too simplistic, and don’t even accept them as useful shortcuts, while they do advocate fast-and-frugal heuristics in a more general context.
Fine then, but what about the problematic cases? Surely we can’t apply models based on the normal distribution to everything? Of course not. But I’m going to tell you a little secret the model critics don’t want you to hear: a modeler is not wed to her model until death do them part. Modelers tend to be quite promiscuous and opportunistic: they switch from one model to another whenever they think that under the circumstances, the one is more appropriate than the other. Where models prove to be weak, they are adjusted, modified, augmented, extended, replaced by or even mixed and used in conjunction with other models (that can be quite an orgy at times, but the result can also be very fertile!). For instance, a quant in an investment bank might use a modified version of Black-Scholes for interest rate options, but switch to a two-factor Hull & White model for interest rate spread options. And no compliance officer who complains!
As a nice illustration of the stark difference between the philosophical quest for truth and market practice, here’s a quote taken from Paul Wilmott on Quantitative Finance (Wiley, 2006) in the chapter on interest rate derivatives (Chapter 32, pp551-552, emphasis added):
These two approaches to the modeling are the consistent way via a partial differential equation or the practitioner way via the Black-Scholes equity model and formulae. The former is nice because it can be made consistent across all instruments, but is dangerous to use for liquid, and high-order contracts. Save this technique for the more complex, illiquid and path-dependent contracts. The alternative approach is, as everyone admits, a fudge, requiring a contract to be squeezed and bent until it looks like a call or a put on something vaguely lognormal. Although completely inconsistent across instruments, it is far less likely to lead to serious mispricings.
3. Conclusion: Pragmatism prevails
At the risk of repeating myself, a model is not meant to present reality as a picture does; to resemble the real thing as closely as possible. A model is grounded in its practical use. Some given model may be ‘truer’ in an abstract philosophical sense, but it may be so impractical as to render it useless. If a modeler relies on unrealistic assumptions, so be it. The ultimate standard by which to judge a model is its performance in the real world. For predictive models the question is: how well are the predictions we can make from it? Even if it’s always theoretically possible to improve on a model, it’s often better to aim for a maximum amount of predictive power with a minimum of computational effort. And never forget that stating an assumption is not the same thing as committing yourself to its literal truth.
The mathematics of models can be quite involved. The mathematical precision of the calculations in working out a model should not be confused with the accuracy of the predictions that result from it. The latter does not only depend on whether the calculations were done properly, but also on a host of other factors; e.g. whether the model is correctly specified (whether important factors are left out, the relation between variables is correctly described and so on), whether its parameters can be reliably estimated and all required initial values of variables are known, and so on. Although a model may be expressed by very abstract mathematics, its function is utterly practical. The main reason for using mathematics is to apply rigor in one’s reasoning. That’s why mathematics is ubiquitous in science, not just in physics. Even a psychologist can’t do without mathematics if she wants to test the efficacy of a therapy rigorously, i.e. in a way that rules out alternative explanations (a patient may feel better for other reasons than that the therapy works).
At the risk of repeating a cliché: finance is not physics. The objects of study are different, by definition. Beyond that, the methods used in physics tend to be different too but the differences are often exaggerated. The great triumphs of physics in terms of stunning predictive accuracy concern only a limited number of applications. Most notably in the field of the very small, like particle physics. Particles can be described by a limited number of properties (mass, speed, electric charge). And they can be isolated from unwanted influences in carefully controlled experiments.
Secondly, some macro-sized objects that inhabit ‘naturally’ isolated systems cannot be controlled but are sufficiently isolated that long-term predictions do not suffer from incomplete descriptions of all the factors and variables affecting them. The prototypical example is our solar system: astronomers’ predictions of the trajectory of planets is made relatively easy by the fact that there’s only one important force at play here – gravity; and the fact that the number of objects affecting each other’s trajectory is relatively small (the gravitational impact of small objects on large objects can be ignored).
But as soon as you turn away from the very small and the very large, and focus instead on phenomena at the human scale, especially in an environment with many influencing factors, you’ll realize that predictions are just as precarious as in finance. If you’re not convinced, try predicting the trajectory of a leaf fallen from a tree on a windy afternoon.
That being said, it doesn’t follow that any attempt of modeling such phenomena is hopeless. Even if a model doesn’t allow precise predictions about specific events (e.g. when will the S&P break the 2000-point barrier?), it can convey very useful information about the qualitative behavior of an agent or system. It can also be used for predictions in a wider sense; predictions involving (long-run) averages or the range of possibilities that can be expected with reasonable confidence. I’ve already hinted at this in the section on Risk Management in part 2, but I’ll explore it in more detail in the next installment of the modeling 101 series.
Coming up next: Part 4: Modeling human behavior – it’s not impossible!
[1] Using elementary calculus you can express the fall time of the object as a function of its distance to the ground upon release:
For d = 100 and g = 9.8, the answer is 4.5 sec.
Or a little bit longer if you attach a parachute. Oops, sorry, I forgot: no air resistance.
[2] You can argue about whether they should be called models, or theories, laws,… The difference is not important here. What’s important is that they all contain simplifying assumptions.
[3] Similar comment as in the previous footnote: some authors make a distinction between the Black-Scholes framework, the model, and the option formula. Again, the distinction is not important for our present purposes.
[4] Dennett has debated Taleb on the topic of religion. See the Hitchens, Harris, Dennett vs Boteach, D’Souza, Taleb debate on YouTube.
[5] Please don’t confuse the mathematical meaning of ‘normal’, as in normal distribution, with its vernacular meaning of ‘usual’ or ‘expected’. The two have got nothing to do with each other, contrary to what normal-distribution haters such as Taleb suggest. The normal distribution derives its meaning from the normal equations in the method of least squares, where normal in that sense means something like ‘orthogonal’. The mathematician Carl Friedrich Gauss (1777-1855) is credited with introducing both the method of least squares and the normal (= Gaussian) distribution in his theory of the motion of planetoids disturbed by large planets.
[6] If you want to read more about this, you can find excellent philosophical/semi-technical articles on philosopher Malcolm Forster’s website.
[7] ‘Free’ parameter in the sense that it can’t be observed directly in the market, in contrast to the riskless interest rate, which has a definite value.
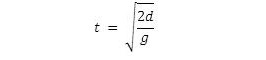
Pingback: MODELING 101 – Part 2 | QUIXOTIC FINANCE