DE GOEDE, DE SLECHTE & DE KNAPPE FEE

Stereotiepe personages zijn een typisch kenmerk van mythen en sagen, legenden en sprookjes: je hebt de goede en de slechte; zwart tegenover wit. De goeden belichamen al het goede en de slechteriken al het slechte. Gemakkelijk te begrijpen voor de kleine kindjes, maar eveneens voor volwassenen die ook wel eens graag een goed verhaal lezen. De neiging om al het slechte en bespottelijke te projecteren op één boeman ligt ongetwijfeld aan de basis van veel moderne mythen.

Zanna Massaert is een ravissante, betoverende columniste die een (bijna) wekelijkse bijdrage schrijft voor het financieel dagblad De Tijd. Waar de doorsnee columnist er hoogstens in slaagt om in binnen de door de redactie streng gerantsoeneerde columnregels ofwel een persoonlijke anekdote te vertellen, ofwel een beleggingstip te geven, ofwel een financiële theorie kort en bondig uit de doeken te doen, doet Zanna alle drie tegelijk – schijnbaar zonder moeite. In enkele recente columns neemt ze de Amerikaanse econoom Fama op de korrel, die volgens haar in Fabeltjesland leeft. (De strompelstap van een dronkenlap, De Tijd, 16 november 2013).

Eugene (“Gene” voor de vrienden) Fama heeft dit jaar de Nobelprijs in de economie gewonnen, samen met Robert (“Bob”) Shiller en Lars Peter (“LP”?) Hansen. Voor wie nog nooit van Fama gehoord heeft, dat is de grondlegger van de Efficiëntemarktenhypothese (EMH), een theorie waarover iedereen een mening heeft (meestal een negatieve), maar die door heel weinigen gekend is. Ik vermoed dat het te maken heeft met het woordje ‘efficiënt’. Het is nogal dubbelzinnig, je kan er gemakkelijk de verkeerde dingen in lezen. In ieder geval, de onpopulariteit van de EMH en het feit dat Fama’s naam en faam eraan verbonden zijn maken van hem een gemakkelijk doelwit voor karikaturisten.

Zanna contrasteert slechterik Fama met haar held Shiller: de eerste gelooft, aldus Zanna, dat extreme bewegingen op de beurs zo goed als onmogelijk zijn (ze gebeuren maar “eens om de 1000 miljard jaar” als je zijn theorie mag geloven, terwijl ze zich in werkelijkheid om de 2-3 jaar voordoen). Shiller daarentegen is zich terdege bewust van de zware staarten in de kansverdeling van beursrendementen (in de ‘staarten’ liggen extreme gebeurtenissen; de ‘dikte’ of ‘zwaarte’ van de staarten is een indicatie van hoe frequent die zich voordoen). Dat beursrendementen geen normaalverdeling volgen, maar eerder een verdeling met zware staarten, is inderdaad een bekend feit. Iemand die dat niet beseft zou je dus in een onvriendelijke bui een idioot kunnen noemen. En als je niet van Fama houdt (om welke reden dan ook) en je wilt hem portretteren als een idioot, wel, dan laat je hem toch gewoon beweren dat beurscrashes zich maar eens om de duizend miljard jaar voordoen. Dat is de enige gedachtegang waarmee ik Fama’s naam kan verbinden aan de uitdrukkelijke stelling dat beursrendementen geen zware staarten vertonen. Maar ik geef toe, mijn verbeelding reikt niet zo ver als die van ervaren verhaaltjesschrijvers.

Wie Zanna’s overtuiging deelt dat Fama in Fabeltjesland leeft zou ik aanraden om eens tegendraads te zijn; doe eens iets dat haast niemand anders doet tegenwoordig, namelijk Fama lezen. Om te beginnen: ‘The Behavior of Stock-Market Prices’ (The Journal of Business, Vol. 38, No. 1. (Jan., 1965), pp. 34-105). Ja dat leest u goed, een artikel van 1965, een jaar waarin Nassim Nicholas Taleb, uitvinder van o.a. het wiel, het warm water, en talloze samengestelde woorden om banale begrippen zwaarwichtiger te doen klinken, nog met de blokjes speelde in de kleuterschool.

Fama was één van de eerste economen (indien niet de eerste) die het werk van Benoit Mandelbrot (Talebs held) onder ruime aandacht bracht; die als eerste een uitgebreid onderzoek deed om Mandelbrots hypothese te testen op financiële data; en, geloof het of niet, de thesis van Mandelbrot bevestigde dat de kansverdeling van beursrendementen niet past in een normaalverdeling met ‘dunne’ staarten. In hetzelfde artikel legt Fama ook uit dat de random walk, een model dat vaak gebruikt wordt om de onvoorspelbaarheid van beurskoersen te motiveren (vandaar Zanna’s titel “strompelstap van een dronkenlap”), niet per se verbonden is aan de normaalverdeling. Een random walk is eigenlijk heel algemeen; als je iedere stap van de dronkaard even groot maakt, en een stap naar voor of achter even waarschijnlijk, dan krijg je inderdaad de normaalverdeling. Maar laat hem een beetje manken op één been, en je krijgt een trend. Laat hem af en toe een sprongetje maken (meestal naar achter), en voor je het weet ligt hij opeens 30 meter achter. Twee citaten uit Fama’s artikel die aan duidelijkheid niets te wensen overlaten:

If the population of price changes is strictly normal, on the average for any given stock we would expect an observation greater than 4 standard deviations from the mean about once every fifty years. In fact observations this extreme are observed about four times in every five-year period. Similarly, under the Gaussian hypothesis for any given stock an observation more than five standard deviations from the mean should be observed about once every 7.000 years. In fact such observations seem to occur about once every three to four years .
[…]

[T]he Mandelbrot hypothesis fits the data better than the Gaussian hypothesis. (Mandelbrot = zware staarten; Gaussian = normaalverdeling , JV)

Mythes en daarmee gepaard gaande vooroordelen kunnen erg sterk zijn. De confrontatie met tegenbewijs roept dan zoveel weerstand (cognitieve dissonantie) op dat men op zoek gaat naar bijkomende verklaringen om het weerspannige bewijs onschadelijk te maken. Met het gevolg dat er extra elementen aan de mythe toegevoegd worden om ze in stand te houden. Onlangs las ik bijvoorbeeld een commentaar op het internet van een criticus die weliswaar op de hoogte was van Fama’s artikel over het gedrag van beurskoersen, maar die dacht dat ergens na 1965 Fama zijn mening moet herzien hebben. Ik vraag mij af of cognitieve dissonantie hiertegen bestand is (Q&A met Fama en Kenneth French in 2009):

Fama: Half of my 1964 Ph.D. thesis is tests of market efficiency, and the other half is a detailed examination of the distribution of stock returns. Mandelbrot is right. The distribution is fat-tailed relative to the normal distribution. In other words, extreme returns occur much more often than would be expected if returns were normal.

Conclusie: dat Fama stelt dat beursrendementen normaal verdeeld zijn is een fabeltje. Meer nog, wanneer Fama in dezelfde Q&A op een bepaald moment iets te lief wordt voor Taleb; met name wanneer Fama enig geloof schijnt te hechten aan Talebs aantijging dat “AIG blew up because its risk model for credit default swaps did not properly account for outlier events“, komt French met de nodige nuancering, daarmee bevestigend dat niet Shiller maar wel Fama alle lof toekomt voor de idee van zware staarten in de financiële economie:

There are lots of academics who are well aware of this issue and consider it seriously when doing empirical research. Those of us who used Gene’s textbook in our first finance course have been concerned with this fat-tail problem our whole careers. Most of the empirical studies in finance use simple and robust techniques that do not make precise distributional assumptions, and Gene can take much of the credit for this as well[…]

Tussen haakjes, voor een meer waarheidsgetrouw relaas van de ondergang van AIG, lees zeker Michael Lewis’ artikel The Man Who Crashed The World. Die man was niet David Li, de boosaardige bedenker van een satanische wiskundige formule die volgens sprookjesschrijver Felix Salmon Wall Street deed crashen, maar wel Joseph Cassano die aan het hoofd stond van AIG Financial Products. Cassano, zo beschrijft Lewis hem, was een autoritair manager met een opvliegend karakter die geen tegenspraak duldde. In tegenstelling tot zijn voorganger had Cassano weinig inzicht noch belangstelling in de wiskundige modellen waarmee zijn afdeling werkte. Toen zijn mensen hem erop begonnen te wijzen AIG FP veel te veel risico’s aan het opstapelen was, werd Cassano kwaad en wuifde hij hun bezorgdheid weg. Zoals ik in mijn vorige post opmerkte, geen enkel wiskundig model is opgewassen tegen des mensen bereidheid om modellen in de vuilbak te smijten zodra die niet langer in hun goed draaiende kraam passen.

Over naar Robert Shiller, één van de pioniers van Behavioral Finance. Voor wie niet vertrouwd is met Behavioral Finance: dat is een financiële theorie die tegenwoordig immens populair is en waarvan de aanbidders elkaar voortdurend bevestigen in de waan dat beleggers een massa kuddedieren zijn, waarboven zij natuurlijk verheven zijn als gevolg van hun selecte inwijding tot de revolutionaire theorie volgens dewelke de mens geen robot is. OK, dat is misschien geen fair beeld van Behavioral Finance, maar nog altijd tien keer fairder dan de populaire kritiek op Fama en zijn EMH. Voor alle duidelijkheid: ik acht Robert Shiller niet verantwoordelijk voor naïeve interpretaties van zijn werk in de brede pers.

Het verdict van Zanna luidt als volgt:

“Ziedaar Fama’s theorie, die vertelt hoe beleggers zouden moeten reageren. Shiller, van zijn kant, toont hoe beleggers echt reageren. Wat blijkt? Fama leeft in Fabeltjesland. Wij zijn lang geen perfect redenerende machines, en al zeker niet in crisistijden”
[…]
“Ziedaar Shillers theorie: extreme situaties komen duizenden keren meer voor dan de Fama-modellen beweren.” (Zanna Massaert, De Tijd, 16 november 2013)

Ziedaar Zanna’s sprookje over Fama en Shiller: Shiller is de legendarische held, de Brenger van het Licht en de Waarheid. Fama is de Boosaard, de Boeman; volgens sommigen bovendien niet alleen verantwoordelijk voor practical jokes zoals het strooien van zand in onze ogen, maar zelfs voor de recente financiële crisis die het gevolg is van “onrealistische modellen die extreme gebeurtenissen onderschatten”.

Tussen haakjes, voor een weerlegging van de mythe van “perfect redenerende machines”, zie ook mijn vorige post waarin ik uitvoerig aantoon dat de veronderstelling van rationaliteit slechts een heel milde aanname is die door geen enkele econoom strikt letterlijk genomen wordt (schijnbaar alleen maar door de tegenstanders); en die nauwelijks invloed heeft op de empirische kracht van economische theorieën. Ook een leuk weetje: kent u de auteur van het onder economen veel geciteerd artikel Inflation, Rational Expectations and the Term Structure of Interest Rates (1973)? Klik maar eens op de link, en kijk goed naar de tweede naam!

Het verbaast mij allerminst dat de gedeelde Nobelprijs voor Fama op veel onbegrip en zelfs verontwaardiging is onthaald, vooral bij mensen die liever sprookjes lezen dan non-fictie.

LACHEN MET DE ZWEDEN

Misschien verbaast het u minder dat Fama de Nobelprijs wint, dan dat Fama en Shiller (plus nog een derde) hem alle drie tegelijk winnen? Is hetgeen Fama vertelt niet rechtstreeks in tegenspraak met wat Shiller vertelt? In dat geval kan maar één van de twee gelijk hebben, en is er eentje bij die hem niet verdient. Zanna merkt hier enige zin voor humor van het Nobelcomité in:

Dit jaar geven ze de hoogste onderscheiding aan iemand die beweert dat de beurs niet te kloppen is en aan nog iemand die beweert dat de beurs wel te kloppen is. Ze krijgen hem allebei voor, ik citeer het prestigieuze communiqué van het nobele juryledencomité, ‘hun empirische analyse van beurskoersen’. Lachen! (nadruk toegevoegd)

M.a.w.: ofwel is de beurs voorspelbaar ofwel niet. Indien niet, dan verdient Fama de prijs; indien wel, Shiller. Maar dat is een naïeve opvatting over economisch onderzoek en weerspiegelt tegelijkertijd een impliciete behoefte aan definitieve, hapklare antwoorden vanwege het groot publiek. Ik vermoed dat het deels om tegemoet te komen aan dat verlangen is dat het comité een weinig geslaagde poging doet om beide visies met elkaar te verzoenen, door Fama gelijk te geven voor wat betreft voorspellingen op de korte termijn, en Shiller op vlak van langetermijnvoorspellingen. De realiteit is echter veel gecompliceerder.

Heeft Shiller bewezen dat men de beurs op lange termijn kan voorspellen? De studie die de juryleden als bewijs voor deze stelling aandragen is ‘Do Stock Prices Move Too Much to be Justified by Subsequent Changes in Dividends?’ (1981). In deze studie toont Shiller aan dat de verhouding koers/dividend (het omgekeerde van het dividendrendement) van de aandelenmarkt over een lange periode schommelt rond een langetermijngemiddelde. Wanneer de ratio dicht tegen de historische bodem aanleunt, dan is de kans groot dat hij terug gaat stijgen. In die zin zou je dus een zekere vorm van voorspelbaarheid kunnen poneren. Er is een grote maar: merk op dat een ratio op twee manieren kan stijgen: via de teller (de koers) of via een daling in de noemer (de dividenden). M.a.w., als je weet dat de aandelenmarkt heel laag noteert in verhouding tot de dividenden die bedrijven uitkeren aan hun aandeelhouders, dan is dat geen reden om al je geld in aandelen te stoppen. De ratio kan ook stijgen doordat steeds meer ondernemingen hun dividenden verlagen of schrappen. Dan heb je misschien een correcte voorspelling gedaan m.b.t. de evolutie van een ratio, maar je hebt er niets aan verdiend.

Het valt niet te ontkennen dat jaarlijkse dividenden veel minder schommelen dan beurskoersen, maar Hansen, de derde laureaat, suggereerde een mogelijk antwoord voor de centrale vraag in Shillers studie: waarom zijn beurskoersen veel volatieler als dividenden? De koers van een aandeel in een rationele prijszetting hangt immers niet alleen af van de winstuitkeringen, maar ook van de verdisconteringsvoet die je gebruikt om de actuele waarde te berekenen van de toekomstige verwachte dividenden. Die verdisconteringsvoet is – een beetje vereenvoudigd – de optelsom van een risicovrije rente en een risicopremie. Hoe groot is die risicopremie? Hoe groot zou die moeten zijn? Geen gemakkelijke vragen, geen gemakkelijke antwoorden.

Heeft Shiller opgemerkt dat er bepaalde patronen te vinden zijn in beursratio’s, Fama zelf heeft eveneens gewezen op bepaalde patronen in aandelenrendementen. Het 3-factor model dat hij samen met Kenneth French bedacht heeft is daarvan een mooie illustratie. Een boeiende discussie in de financiële economie gaat over de interpretatie van bovengemiddelde rendementen. Wanneer puur toeval als verklaring is geëlimineerd, dan kan men zich afvragen of het extra rendement het bewijs is van een inefficiënte markt of misschien eerder wijst op een verborgen risico. Bijvoorbeeld, één van de drie Fama-French factoren is de kapitalisatie van een aandeel: small-caps blijken op de lange termijn beter te presteren als large-caps. Men zou dat kunnen interpreteren als een gat in de markt voor de snuggere belegger, maar eveneens als vergoeding voor het extra risico dat gepaard gaat met small-caps (o.m. hun beperkte liquiditeit). Het laatste woord is daarover nog lang niet geschreven.

Bij het toekennen van de Nobelprijs hebben de juryleden inderdaad benadrukt dat de drie laureaten een grote bijdrage hebben geleverd tot ‘de empirische analyse van beurskoersen’, zoals Zanna opmerkte. Dat ze daarbij niet altijd tot dezelfde conclusies komen is echter geen tegenstrijdigheid, maar wel een bewijs voor het feit dat heel algemene uitspraken m.b.t. tot de economische werkelijkheid niet met één smoking-gun studie bewezen of weerlegd worden. Wat een beetje onderbelicht wordt in de polemiek “efficiënt versus niet-efficiënt” (hoewel de juryleden van het Nobelcomité het vermelden in hun motivering) is dat alle drie de laureaten een uiterst vruchtbare erfenis hebben nagelaten voor hun collega’s: zij hebben namelijk een heel arsenaal van technieken ontwikkeld om beursrendementen te analyseren. Ook al zijn ze het inhoudelijk vaak oneens, meestal bestaat er wel een duidelijke consensus over de waarde van de gebruikte methoden.

Waar Zanna het volgende fabeltje gehaald heeft heb ik niet kunnen achterhalen:

Lars Peter Hansen krijgt de prijs omdat hij een systeem heeft bedacht waarmee je prijzen kan voorspellen zonder dat het allemaal zo correct hoeft te zijn. Een ‘redelijke schatting’ is al lang goed. […] De beurs zal stijgen of ze zal dalen, behalve als ze niets doet. Altijd prijs. Op 10 december in Stockholm op te halen. (nog altijd Zanna in dezelfde editie van De Tijd)

Zanna entertaint haar lezers met financiële weetjes zonder dat het allemaal waarheidsgetrouw hoeft te zijn. Pret gegarandeerd!

DE JACHT OP BLACK & SWANS

Zanna leest niet enkel voor het amusement boeken over financiële theorie, nee hoor, ze weet er altijd een nuttige beleggingstip uit te distilleren:

Shillers klok heeft ‘zware staarten’. Dat is goed nieuws, want met zware staarten valt veel aan te vangen. Een zelfversterkende crisis of euforie is een flinke overdrijving. Nadien, als hij zijn roes heeft uitgeslapen, zal de dronkenlap wel weer naar een min of meer evenwicht terugkeren. Na een crash volgt een herstel, na een boom volgt een correctie. (Nog steeds dezelfde column van 16 november)

Na regen komt zonneschijn, een waarheid als een zwarte koe. Maar je kan wel behoorlijk nat worden als je na vijf dagen regen met deze gedachte zonder paraplu naar buiten gaat. In elk geval, de idee van zware staarten herbergt helemaal geen ‘terugkeer naar een evenwicht’. Eerder het tegendeel: wat tail-events (extreme gebeurtenissen) zo verraderlijk maakt is dat ze nog veel meer dan normale fluctuaties een formidabele uitdaging bieden aan iedereen die zich waagt aan voorspellingen op basis van evenwichten, of aan voorspellingen tout court.

(vervolg van vorig citaat:) Bon, hoe speelt een Zanna daar nu op in, via een glashelder, poepsimpel en (nog) nergens anders toegepast trucje? Het antwoord, beste lezer, is voor volgende week.

Zanna houdt haar beloften: het antwoord volgde in haar column van 23 november (“Het Model van Black en Decker“, De Tijd). Menig trouw lezer heeft vol spanning het moment afgewacht waarop Zanna haar poepsimpele beleggingsformule uit de doeken zou doen, en zeven nachten wakker geleden van de vraag waarom de honderdduizenden professionele beleggers die continu de markten afschuimen naar gouden opportuniteiten ze nog niet ontdekt laat staan toegepast hebben.

Waarom zijn er zoveel meer extreme beursbewegingen dan modelmatig wordt aangenomen? Omdat de theorie achter extreme bewegingen te moeilijk is, daarom. Probeer maar eens emoties in een model te duwen. Je geraakt daar niet uit wijs. (Zanna in De Tijd, 23 november 2013).

Psychologen hebben nochtans wel degelijk modellen voor emotioneel gedrag. Maar de reden dat die niet veel gebruikt worden in de financiële economie (in tegenstelling tot misschien de micro-economie) is wellicht dezelfde dat het atoommodel van Bohr niet gebruikt wordt in de psychologie, ondanks het feit dat het menselijk lichaam opgebouwd is uit atomen: omdat emoties een eigenschap zijn van mensen, niet van atomen. Emoties zijn evenmin een eigenschap van beurskoersen; de beurs wordt niet kwaad, de beurs wordt niet ongeduldig, enz. Beleggers wel uiteraard, maar de conclusie dat je geen beurskoersen kan modelleren zonder rekening te houden met de emoties van beleggers is net zozeer een non sequitur als het argument dat je onmogelijk de werking van een motor kan beschrijven zonder rekening te houden met de sterke kernkracht die protonen en neutronen in een atoomkern samenhoudt.

Samengevat luidt de redenering van Zanna als volgt:

1. De theorie van extreme bewegingen is te moeilijk.
2. Bijgevolg gaan financiële modellen er gemakshalve van uit dat extreme bewegingen niet vaak voorkomen.
3. Die modellen worden algemeen gebruikt.
4. Bijgevolg wordt de kans op extreme bewegingen schromelijk onderschat.
5. Dat uit zich onder andere in systematische ‘fouten’ in marktprijzen van sommige beleggingsinstrumenten.

Mijn commentaar op elk van de stappen in het argument:

1. Het modelleren van extrema is weliswaar moeilijker dan het modelleren van gemiddelden, maar dat neemt niet weg dat er een volumineuze literatuur over bestaat, van de eerder genoemde fat-tailed distributions tot bijvoorbeeld Extreme Value Theory. Wat voor de leek ingewikkeld is, is het daarom nog niet voor de ervaren academicus.
2. Dat doen sommige modellen inderdaad, bijvoorbeeld modellen die gebruikt worden voor toepassingen waarbij de frequentie van extreme gebeurtenissen van weinig belang is.
3. Zie (2). Normaalverdelingen worden gebruikt in elke tak van de wetenschap. Maar dat wil niet zeggen dat de beperkingen ervan onderschat of miskend worden. In tegenstelling tot wijd verspreide mythen en fabeltjes werken wetenschappers zelden met één enkel model. Ze hebben ook een heel arsenaal van kansverdelingen tot hun beschikking, waaruit ze de meest geschikte kiezen naargelang het probleem dat ze moeten oplossen.
4. In elk geval niet door degenen die zich professioneel bezig houden met het modelleren van financiële data.
5. NU wordt het interessant!!

Ja zeker, want nu volgt Zanna’s gouden beleggingstip waarop haar lezers 7 lange dagen en nachten in volle spanning hebben zitten wachten:

De prijzen van die opties zijn gebaseerd op die welbekende modellen die extremiteiten te weinig in rekening brengen. Zoek dus extremiteiten op. Koop opties op een koers die binnen een tijdsbestek waarschijnlijk niet zal worden bereikt. (nog steeds
Zanna in De Tijd van 23 november 2013).

Zanna verwijst hier naar de formule van Black & Scholes (vandaar de titel van haar column: “Het Model van Black en Decker”), een vaak gebruikte formule om opties op aandelen of andere beleggingsinstrumenten te waarderen. Hiermee volgt ze het advies van de nr. 1 mythomaan in de populaire financiële media: Nassim Taleb. Taleb is een productief sprookjesschrijver, alleen blijkt het voor zijn talrijke fans moeilijk te zijn een onderscheid te maken tussen ‘s mans fantasie en de werkelijkheid.

Alle mogelijke misvattingen over modellen vind je terug bij Taleb. Economen beschuldigen dat ze wereldvreemde nerds zijn die geen voeling hebben met de realiteit is eveneens zijn handelsmerk. Aan Talebs misvattingen m.b.t. Black & Scholes ga ik zeker nog een artikel wijden op deze website, maar voor de lezer die niet zo lang kan wachten volgt hieronder al een korte samenvatting.

De Black-Scholes formule geeft de ‘faire’ prijs van een aandelenoptie op basis van een aantal inputvariabelen: de vervaldatum van de optie, de koers van het onderliggend aandeel, de volatiliteit van datzelfde aandeel, de uitoefenprijs van de optie, eventueel het dividendrendement van het aandeel, en de risicovrije rente (vb. rente op staatsobligaties). Ergens in de formule wordt gebruik gemaakt van de normaalverdeling. Dat heeft inderdaad tot gevolg dat een naïef gebruik van de formule zou leiden tot optieprijzen die de kans op extreme gebeurtenissen onderschatten, en bijgevolg veel te duur of veel te goedkoop zijn, naargelang de aard van de optie. So far so good.

Wat Taleb echter heel goed weet (hij is namelijk zelf nog trader geweest), is dat de Black-Scholes formule net om die reden nooit op zo’n naïeve manier gebruik wordt; lees bijvoorbeeld het artikel dat hij samen met Espen Gaarder Haug schreef: Why We Have Never Used the Black-Scholes-Merton Option Pricing Formula. Zoals hij zelf opmerkt passen traders een inputvariabele aan om de formule de gewenste uitkomst te laten geven, namelijk een optieprijs die wél rekening houdt met extreme gebeurtenissen. De inputvariabele die daarvoor gebruikt wordt is de volatiliteit, de enige variabele die niet rechtstreeks observeerbaar is in de markt. Dat leidt tot de zogenaamde volatility smile: een gebogen curve die de door de markt gehanteerde volatiliteit afzet tegen de uitoefenprijs van opties op hetzelfde onderliggend aandeel en met dezelfde vervaldatum. Zo zal je zien dat een call-optie op bijvoorbeeld Google met uitoefenprijs 1000 dollar een heel andere volatiliteit inprijst dan één met een uitoefenprijs van 1.300 dollar. Op het eerste gezicht is dat een uiting van inconsistentie in de markt: er is namelijk maar één enkele volatiliteit voor het aandeel Google, dus waarom is er een hele curve van volatiliteiten in functie van optiekenmerken?

Voor Taleb is het niet meer als dat: een ‘fudge’, een geknoei zeg maar, om een modelmatige berekening van de optieprijs in overeenstemming te brengen met de werkelijke koers. Geknoei, en dus ongeoorloofd. Maar dat is de zaken op zijn kop zetten. Traders gebruiken de formule niet om op basis van een schatting van de volatiliteit de faire (modelmatige) waarde van de optie te berekenen, om vervolgens opties te kopen waarvan de berekende faire waarde hoger ligt dan de marktprijs. Integendeel, marktprijzen zijn het uitgangspunt; de formule wordt gebruikt in de omgekeerde richting: om de “impliciete” volatiliteit te berekenen op basis van de marktprijs. In feite is de impliciete volatiliteit gewoon een andere manier om de prijs van een optie weer te geven. Een veel handigere manier ook, die vergelijkingen tussen opties met verschillende karakteristieken vergemakkelijkt. Vergelijk het met het de gewoonte om obligaties te quoteren in rendement (yield-to-maturity) naast een prijs als percentage van de nominale waarde (bijvoorbeeld 101%).

Waarom het op die manier doen? Waarom niet gewoon een realistischer model gebruiken om opties te waarderen? Zulke modellen bestaan, maar zijn vaak zo ingewikkeld dat ze totaal onpraktisch zijn. Uitbreidingen van of alternatieven voor Black & Scholes worden wel gebruikt voor zogenaamd ‘exotische’ (meer ingewikkelde, minder courante) producten.

Voor de leek klinken de vorige paragrafen wellicht erg ingewikkeld, maar de voornaamste boodschap is heel eenvoudig: de beperkingen van de Black-Scholes formule zijn algemeen erkend, en de markt heeft al 25 jaar geleden een manier gevonden om de grotere kans op extreme gebeurtenissen toch tot uiting te laten komen in optieprijzen, namelijk via de impliciete volatiliteit. Rechtstreeks gevolg hiervan is dat wie denkt in de optiemarkt een free-lunchrestaurant gevonden te hebben, wel eens met serieuze buikpijn (en een lege portemonnee) kan thuiskomen.

DE AVONTUREN VAN ZANNA IN NYRSTAR

Om te profiteren van de vermeende mispricing van opties kocht Zanna 10 call opties op Nyrstar met een uitoefenprijs die ver boven de huidige koers ligt (uitoefenprijs van de optie: 3,40 euro – koers van het aandeel: +/- 2,20 euro). Die opties zijn op vervaldatum september 2014 nul komma nul euro waard indien het aandeel van Nyrstar op dat moment minder dan 3,40 euro waard is. Natuurlijk hoeft ze haar opties zolang niet bij te houden. Als Nyrstar intussen sterk stijgt kan Zanna ze met winst verkopen. Misschien.

Ze betaalde 0,14 euro per optie. Dat bedrag vermenigvuldigd met 1000 ( 10 opties x 100, omdat één optie recht geeft op honderd onderliggende aandelen Nyrstar) geeft 140 euro in totaal. Daar komt nog eens 30 euro transactiekosten bij, inderdaad een ‘gepeperde’ rekening zoals ze zelf zegt. Reken nog eens op 30 euro transactiekosten bij een verkoop, en je komt aan een totaal kostenplaatje van 60 euro voor een inleg van 140 euro. Dus de opties moeten al minstens 43% stijgen om break-even te spelen. Dat wil natuurlijk niet zeggen dat het aandeel 43% moet stijgen, want opties bevatten een hefboom waardoor ze sterker stijgen dan het onderliggend aandeel (in geval van call-opties).

Maar dat zijn alleen nog maar de zichtbare kosten. Nog veel sterker gepeperd zijn de verdoken kosten voortvloeiend uit de astronomische bid-ask spreads op de Brusselse optiebeurs, vooral voor sterk out-of-the-money opties (opties met een uitoefenprijs ver boven de huidige aandelenprijs, zoals in dit geval). Ter illustratie, dit is de bid-ask spread voor Zanna’s optie op Nyrstar, twee weken na haar aankoop:

Bied: 0,09 euro

Laat: 0,19 euro

Wat dit betekent is het volgende: u koopt aan de laatkoers, dus 0,19 euro. Wilt u de optie meteen opnieuw verkopen krijgt u er slechts 0,09 euro voor terug (biedkoers is de koers die marktmakers bieden wanneer u wenst te verkopen). Een verschil van zomaar eventjes 0,10 euro, oftewel 100 euro verdoken kosten bij een aankoop van 10 opties. Tel dat op bij de 60 euro transactiekosten en je krijgt een totaalbedrag van 160 euro bovenop de nettoprijs van 140 euro voor de opties zelf. Dergelijke belachelijke bid-ask spreads zijn typisch voor een extreem illiquide markt. Hoe illiquide wordt meteen duidelijk uit de historiek van eind september tot eind november van de volumes (aantal verhandelde opties) van Zanna’s call optie op Nyrstar:

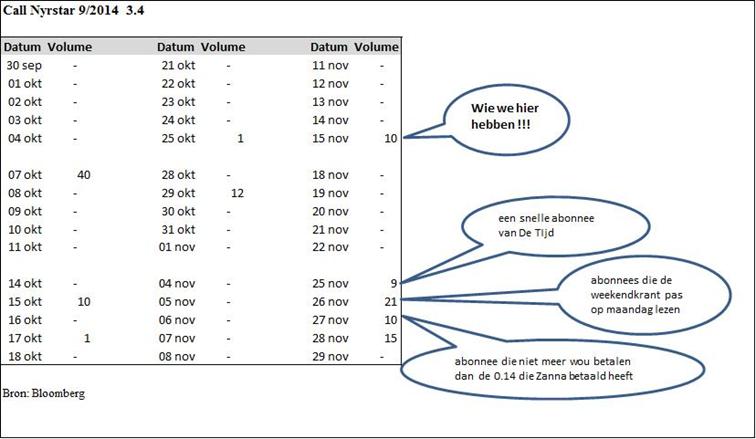
Op zaterdag 23 november schrijft Zanna dat ze “vorige week” 10 opties gekocht heeft. Uit de bovenstaande figuur blijkt dat haar transactie de enige die week was (vrijdag 15 november), na meer dan twee weken zonder dat er maar één optie van handen wisselde. Zanna’s column heeft in elk geval terug wat leven in de brouwerij gebracht, want in de week van maandag 25 november t/m vrijdag 29 november worden zomaar eventjes 55 opties verhandeld, meer dan het dubbele van de hele maand voordien!

Zanna ziet er veel te braaf uit om ze te verdenken van koersmanipulatie (hoewel ze ook wel een stout kantje heeft – zie hierboven), maar ik zou toch maar voorzichtig zijn als ik haar was. De FSMA leest ook De Tijd (in de momenten dat ze niet op Quixotic Finance zitten).

Nu is de Brusselse optiebeurs wel een topper op het vlak van illiquiditeit, maar als je kijkt naar de bid-ask spreads van opties op Nasdaq, dan zal je merken dat die eveneens erg hoog liggen voor sterk out-of-the-money opties. Geen wonder dat market-making een lucratieve activiteit is, ook al strijkt er om de 2-3 jaar een zwarte zwaan neer.

‘TAFELTJE DEK JE, EZELTJE STREK JE’ & GELIJKAARDIGE SPROOKJES

Wat beleggingsfabeltjes zo aantrekkelijk maakt is dat ze ons een eenvoudige manier om geld te verdienen voorspiegelen. Free lunches voor iedereen die niet gelooft in de rationaliteit van de markt. Vreemd toch dat we na zoveel jaren behavioral finance en Black Swan hype geen massaal verschijnen zien van beleggers die rijk zijn geworden dankzij Shiller of Taleb. Talebs eigen hedge funds hebben een kortstondig leven gehad (zoals de meeste hedge funds trouwens), iets waarvoor hij in de loop der jaren een aantal tegenstrijdige verklaringen heeft gegeven (waarvan de allerleukste: “Ik heb het geld niet nodig”).

Even aantrekkelijk is het fabeltje dat een halfbakken filosofisch argument volstaat om het werk van meerdere generaties economen naar de prullenmand te verwijzen. Niet nodig om statistiek of wiskunde te studeren, niet nodig om grondig onderzoek te verrichten naar de werking van financiële markten, niet nodig om massa’s data te verzamelen en die op alle mogelijke manieren nauwgezet te analyseren; gewoon boekjes lezen van schrijvers met veel meer pretentie dan inhoud, en de rest komt vanzelf. Geestelijke verarming bedoel ik dan.

Moraal van het verhaal: hoed u voor fabeltjes. Wanneer iemand u een free lunch tracht te verkopen (of die lunch nu van financiële of intellectuele aard is), vraag u dan altijd af waarom duizenden professionele beleggers of academici met kennis van zaken er hun neus voor ophalen.